Log X is Lipschitz Continuous on 0
5_ Let f (x) Vx _ (i) Show that f is not Lipschitz continuous 0n [0, 1]. (ii) Find a sequence { fn} of Lipschitz continuous functions on [0, 1] which converges uniformly to f. (Prove your claims! )

Related Question
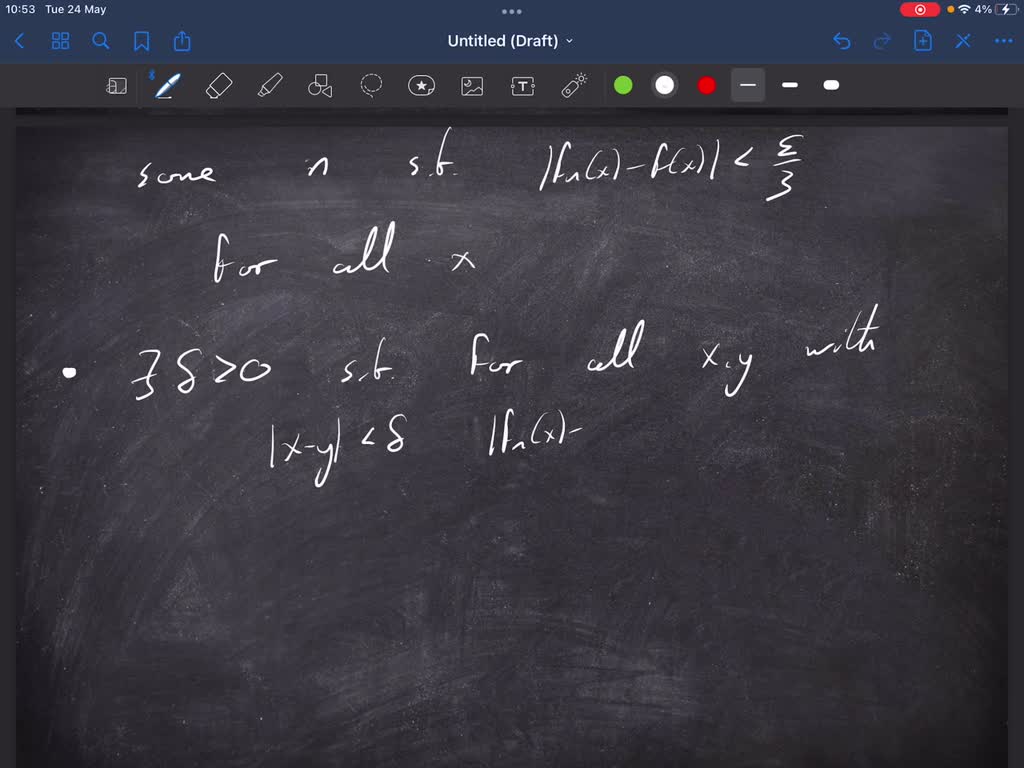
8. Prove that if {fn} is & sequence of uniformly continuous functions on & set D and if this sequence converges uniformly to OnI D, then f is also uniformly continuous_
Discussion
You must be signed in to discuss.
Video Transcript
Okay, so we have some functions F N which are uniformly continuous. We're told that FN converges to F uniformly. We want to show that this means F is also uniformly continuous. So for the sake of this proof, I'm going to do everything with real functions and take absolute values. But if you want to generalize this, you can just put a norm or a metric and the proof is exactly the same, but I'm just going to put absolute values to make things a little bit easier on notation. So the first thing to notice is that we need to prove the following, we need to prove that for all epsilon greater than zero, There exists Delta greater than zero. Such that for all X Y. Such that x minus Y is less than delta. We have F of x minus F of Y is less than epsilon. So this is what we want to show notice. This is the definition of uniform continuity because we have all xy here, not just for some fixed X. And then changing Y. So this is the definition of uniform continuity. So the first thing we're going to use is the fact that F N converges to f uniformly. So we're going to fix epsilon greater than zero to write all of this and no sense F N converges to F uniformly. There is some and such that F n of x minus F of X is less than ε over three for all X. So by definition of uniform continuity, we can find some F N function which is within epsilon over three for all X. And again for all X is important here. Now we're going to use the fact that F n each f n function is uniformly continuous. So in particular, this one is, so by uniform continuity There exists Delta greater than zero. Such thoughts for all X Y with x minus y less than delta. We have F of x -5 of Y is less than epsilon over three. And then finally, we can combine these two things to finish the proof. So we'll say all X Y with x minus Y less than delta. We need to look at the difference of F and F of x minus F of Y and show that this is less than epsilon. So we're going to just use the trick of adding and subtracting zero here. So we're gonna try, this is F of x minus F of Y plus F N of x -5 of X plus F n of y -5, And then we can group terms together. In a nice way, we can group F of x minus f N of X. That these two terms we can group. So let's put brackets here, we can group F of Y and F of Y. So we'd get F N of y minus F of Y here. So that's these two terms. And finally we have so let me move this slightly plus F N of X mindless F N of Y. Now we can use the triangle inequality to break this up and leave us with F of x minus f n F Y f n of X plus f n of y minus F of Y plus f n of x minus f n of Y. No, these two terms here are going to be less than epsilon over three by the first bullet point up here because this is true for all X. So it's true for X. And why here? So this is less than epsilon over three plus epsilon over three. And here this term is going to be less than ε over three by this bullet point here. So this is plus epsilon over three overall Adonis. Together we get upsilon. So we've shown that if we let epsilon be greater than zero, then there is some delta. Such that So the delta it comes from this choice here for all X. Y with x minus Y less than delta. We have F of x minus F of Y is less than asylum. So F is uniformly continued
Source: https://www.numerade.com/ask/question/5_-let-f-x-vx-_-i-show-that-f-is-not-lipschitz-continuous-0n-0-1-ii-find-a-sequence-fn-of-lipschitz-continuous-functions-on-0-1-which-converges-uniformly-to-f-prove-your-claims-76154/

0 Response to "Log X is Lipschitz Continuous on 0"
Post a Comment